递归确实是一种较为抽象的数学逻辑，可以简单的理解为程序调用自身的算法。

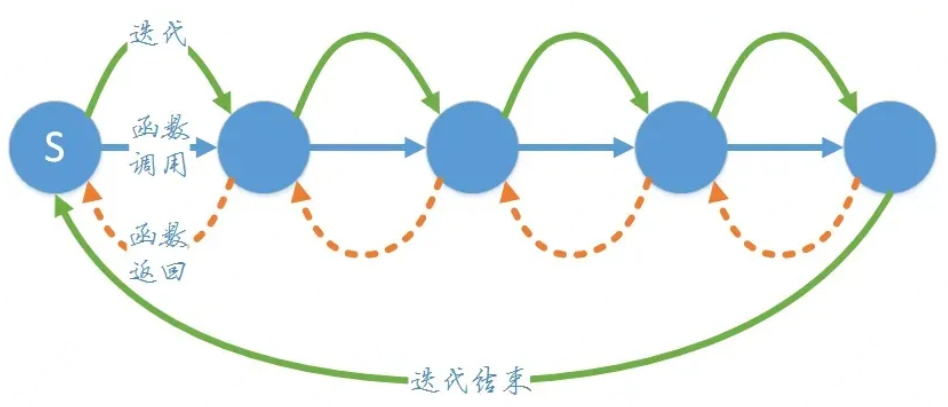
递归的运行逻辑

• 函数直接或者间接调用自身就是递归
• 递归需要有边界条件、递归前进段，递归返回段

• 递归一定需要有边界条件

• 当边界条件不满足的时候，递进前进
• 当边界条件满足的时候，递归返回

递归一定要有退出条件，递归调用一定执行到这个退出条件。没有退出条件的递归调用，就是无限调用，递归调用的深度不宜过深

维基百科对递归的解释是：

 递归（英语：Recursion），又译为递回，在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。
例如，当两面镜子相互之间近似平行时，镜中嵌套的图像是以无限递归的形式出现的。也可以理解为自我复制的过程。

"递"是传递的意思，"归"是归还的意思，先把一个方法一层层传递下去，然后传递到最后一层再把结果归还回来。

比方说我排队做核酸检测，前面有100个人，我想问下医务人员几点下班，于是问了我前面那兄弟，他又问了他前面的人，一个个传递下去，最终传递到了医务人员那里，回话说下午六点下班。这句话又往回传，最终到了我这里，我知道了医务人员六点下班。

这个过程就是一个递归过程，如果说"传话"本身是一种方法，那这整个传话过程就是在调用自身方法，最终获得了结果。

这和循环不一样，循环相当于给所有人都所有人都戴了耳机，然后有"中介"挨个去问你知道医务人员几点下班吗，等问到医务人员的时候，得到答案，“中介”告诉我六点下班。

实质上，递归就是把一个大问题不断拆解，像剥洋葱一样，最终拆解到最小层面，会返回解题结果。

用Python举一个最简单的递归函数例子，讲一讲什么是递归的应用。

我们经常会看到函数会调用自身来实现循环操作，比如求阶乘的函数。

整数n的阶乘即n*(n-1)*(n-2)*...*3*2*1

如下面5行Python代码，就能实现阶乘的计算

很多人可能困惑这里面的计算逻辑，为什么factorial函数中调用了自身，最终能得到结果。

我们可以按照数学逻辑进行推演：

整数n的阶乘是：fact(n) = n*(n-1)*...*3*2*1

整数n-1的阶乘是：fact(n-1) = (n-1)*(n-2)*...*3*2*1

所以可以推断 fact(n) = n*fact(n-1)

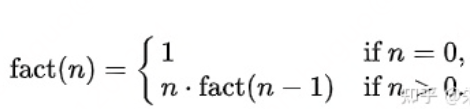
这里是不是一种 fact方法可以为每个数所调用，最终调用到了n=1的时候，就返回结果n的阶乘。

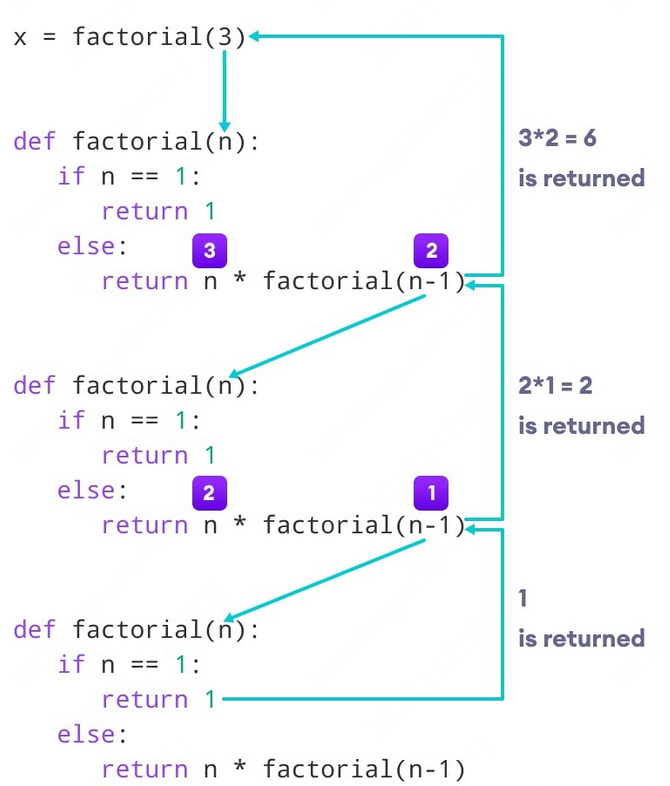
大家看上图，递归函数会一层层往下调用，最终到n=1的时候，往上返回结果。

这就是递归的全过程，如果我们给递归下一个准确的定义，可以概括为以下3点：

1、至少有一个明确的递归结束条件；

2、给出递归终止时的处理办法；

3、每次进入更深一层递归时，问题规模(计算量)相比上次递归都应有所减少

以上面代码为例：

def factorial(n):
    ''' n表示要求的数的阶乘 '''
    if n==1: # 1、明确递归终止条件；
        return n # 2、递归终止时的处理办法
    n = n*factorial(n-1) # 递去
    return n  # 归来

除了常见的阶乘案例，还有斐波那契数列，也是递归的经典用法。

斐波那契数列：1，1，2，3，5，8，13，21，34，55，89...

这个数列从第3项开始，每一项都等于前两项之和。

它以如下被以递推的方法定义：F(0)=0，F(1)=1,F(n)=F(n - 1)+F(n - 2)（n≥ 2，n∈ N*）

在Python中，我们可以使用递归函数的方式去实现斐波那契数列。

除了数学的解释，之前也看到有人对递归更加形象的解释：

1、我们已经完成了吗？如果完成了，返回结果。如果没有这样的终止条件，递归将会永远地继续下去。
2、如果没有，则简化问题，解决较容易的问题，并将结果组装成原始问题的解决办法。然后返回该解决办法。

大家是不是对递归有了一个更加深刻的认识，如果还不清楚，没关系，这里还有更多的递归案例，用Python来实现，可以说非常简洁。